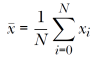Garbage in, garbage out

Los datos de entrada son una parte muy importante del machine learning.
Si los datos con los que vamos a entrenar nuestro modelo no son una buena representación de los datos que usará el modelo en producción, no conseguiremos que tenga un buen rendimiento. Este apartado va de cómo conseguir un buen conjunto de datos o “dataset”.

Uno de los problemas a resolver por la IA son de “clasificación”: clasificar los datos de salida de nuestro modelo en categorías o clases.
A estas clases se les asigna un identificador o etiqueta, que también puede ser un valor numérico para trabajar con ellas.

Con “feature” (“la traducción literal es “característica” o “atributo”) nos referimos al significado físico que representa un dato. Suelen ser numéricos para poder usarlos con los modelos.
Estas características representarán alguna cosa, en función del problema a resolver (medidas, imágenes, etc).

Me referiré a estas “Features” indistintamente como “features”, “características”, “características de datos”, “datos” o “atributos”.

Los features pueden ser valores medidos, o cualquier otra cosa. Los feature vectors (“vectores de características”) son agrupaciones de estos datos usados como entradas a nuestro modelo.
Antes de introducir estos feature vectors es común tener que manipularlos para adaptarlos a la entrada del modelo.

Número “decimales”, o mejor expresado “números reales”. Al tener valores decimales representan valores continuos.

Estos números son enteros, es decir, sólo pueden tomar valores discretos con un determinado gap o “espacio” entre uno y otro.
Si la diferencia, o intervalo, entre cada posible valor es siempre el mismo, estos números son denominados “valores de intervalo”.

En este caso, los números que identifiquen los elementos de entrada, aunque sean consecutivos, pueden representar cosas que no tengan una diferencia o intervalo idéntico.
Podemos usar valores numéricos enteros en una entrada, en los que cada uno pueda representar cosas (por ejemplo diferentes grados de estudios, denominaciones de bienestar económico, etc) cuya diferencia de un valor al siguiente, no tenga por qué ser idéntico matemáticamente (ni se le pueda dar esa definición) en todos los casos (ejemplo: 1 sin estudios - 2 estudios primarios - 3 estudios secundarios - 4 estudios universitarios).

Este tipo de valores se refiere a codificar numéricamente una categoría para poder ser usada como entrada para el modelo, sin que haya relación directa entre categorías (no son valores ordinales).

Sin embargo nuestros modelos podrían usar estos datos como valores ordinales. Para evitarlo, podemos crear por cada elemento un vector en el que cada posición sólo puede tomar valores binarios, en el cual haya un dígito por cada posible categoría. De esta forma todos serán 0, salvo el dígito que represente la categoría, que será 1.

El problema de este sistema es que puede dar lugar a vectores realmente grandes, por ejemplo: sexo: vector de 2 elementos, 5 posibles colores: 5 elementos, miles de posibilidades: miles de elementos por vector.

Usando esta estructura, si tenemos una matriz que representan las entradas, cada una especificada por cada fila, sólo habría una posición con '1' en cada fila. Por ello, este enfoqe se denomina One-shot encoding.

Feature selection: La selección de atributos es el proceso en el que se seleccionan los datos que se pasarán a los vectores de datos que servirán para entrenar nuestro modelo.
El vector de datos debe contener sólo las características de datos (magnitudes, categorías, etc) que contengan información que permitan generalizar al modelo para funcionar con datos nuevos. Es decir, que permitan al modelo diferenciar entre clases.

Hay que se cuidadoso porque necesitamos seleccionar suficientes de estas características (datos de entrada) que permitan al modelo “aprender”, pero si seleccionamos demasiados tendremos problemas con la “maldición de la dimensionalidad” Curse of dimensionality.

Curse of dimensionality: Cada característica de datos que añadamos a nuestro vector de datos, aumentará éste en una dimensión. Si tenemos 2 datos de entrada podríamos representar cada vector en un eje XY. Si fueran 3, en un eje XYZ. Más de tres sería un especio multidimensional no representable gráficamente.

Para tener una muestra lo suficientemente significativa para que el modelo funcione correctamente al recibir cualquier nuevo dato, los datos de entrenamiento deberían distribuirse por todo el espacio multidimensional. Para comprobar esto dividimos cada dimensión en 10 partes (bins): 2 dimensiones serán 100 partes, 3 dimensiones 1000, 4 dimensiones 10.000, etc.
Una vez dividido comprobamos en cuantas partes bins hay un dato para ver cuántas partes están ocupadas por datos. Si tomamos 100 datos aleatorios, para 2 dimensiones obtendremos aproximadamente un 41% de partes ocupadas con datos. Para 3 dimensiones un 4,8%. Para obtener un valor significativo similar al de 2 dimensiones, necesitaríamos unas 1000 muestras para 3 dimensiones.

En función del número de dimensiones de los elementos del vector de entrada, necesitaremos más muestras para entrenar a nuestro modelo, normalmente asumidas como aproximadamente 10^d, donde d es el número de dimensiones.

Según esto, podemos ver un ejemplo:
Usamos como entrada una imagen en color. Esta imagen tendrá 1024 píxeles de largo por 1024 píxeles de ancho. Y cada píxel tiene 3 colores de 1 byte de intensidad por cada color RGB. De esta manera el feature vector tendrá: d = 1024 x 1024 x 3 = 3.145.728 dimensiones (nº de elementos). Necesitaríamos aproximadamente 10^3.145.728 muestras de datos. Esto simplemente, no es posible.

Sin embargo, ese número tan brutal, lo que indica realmente son todas las posibles combinaciones que podemos hacer con una cantidad de dimensiones tan elevada. En el caso de una imagen, la mayor parte de estos valores es ruido. En realidad, el conjunto de imágenes existentes es un número mucho menor que el de todas las imágenes posibles.

Este problema paralizó la investigación en inteligencia artificial durante décadas, pero en la actualidad hay formas de evitarlo, aunque sigue siendo necesario tenerlo en cuenta para modelos tradicionales.

Un dataset es una colección de pares de valores {X, Y}, donde X es el input del modelo e Y es la etiqueta label resultante.

En el aprendizaje supervisado el dataset es una colección de ejemplos, y el entrenamiento consiste en que el modelo sea capaz de minimizar todo lo posible el error en el etiquetado, para ese dataset.

Interpolación es el proceso de estimar un resultado dentro de un rango conocido.
Extrapolación es el proceso que se da cuando se usan los datos para obtener una salida de un dato fuera del rango conocido.

Es decir, entrenamos al modelo con un dataset que debe ser una muestra representativa que permita predecir salidas o etiquetados. Si el dato de entrada se encuentra dentro del rango de datos del dataset, hablamos de interpolación. Si el dato de entrada se encuentra fuera del rango de datos cubierto por el dataset, hablamos de extrapolación.

El dataset debe ser representativo de las clases que se están modelando. Se asume que nuestros datos tienen una “distribución principal”, esto es un generador de datos desconocido que creó el dataset particular que estamos usando. La “distribución principal” es un ideal de la distribución perfecta para modelar las clases que deseamos, de forma que el dataset que manejamos “ha sido extraído” de ésta de una forma estadística desconocida.

Esta es una idea casi “filosófica” pero que tiene sentido matemático. Los resultados del modelo tienen un sentido estadístico, que son el resultado de la “distribución principal” de los datos de entrada. Los datos de entrada, los datos de test y los que le pasamos al modelo para tomar decisiones, deben venir de la misma “distribución principal”.

Puede ser sencillo incurrir en errores y entrenar un modelo con datos de una “distribución principal”, y testearlo o usar datos de entrada de otra diferente.
Cómo usar un modelo con datos de una “distribución principal” diferente a la de los datos con los que ha sido entrenado, es un campo de investigación actual denominado domain adaptation.

La llamada prior class probability o probabilidad de clase anterior, se refiere a la propiedad de que cada clase aparezca en nuestro modelo. En general, deseamos que nuestro dataset coincida con con la probabilidad en que las clases aparecieron anteriomente.

Por ejemplo, si por norma general, una clase aparece aproximadamente el 85% de las veces, y otra el 15%, deseamos que nuestro dataset incluya las clases en la misma proporción.

El problema se da cuando una clase aparece muy pocas veces (por ejemplo una cada 10.000 entradas), ya que el modelo probablemente aprenderá muy bien la más habitual, pero cuando aparezca una diferente, probablemente fallará debido a que no ha tenido suficientes de estos datos para entrenar.

Una forma de salvar este problema es el de entrenar el modelo una en una proporción 10:1 con el modelo que menos aparece, y cuando haya pasado un tiempo, aumentar la proporción hasta obtener la real.

Este “truco” no funciona con todos los modelos, pero sí con redes neuronales. Podemos intuir, que primero aprende la clase, y después al variar la cantidad de veces que aparece, el modelo aprende la periodicidad con que aparece.

Los “trucos” y técnicas empíricas funcionan muy bien en machine learning, especialmente en deep learning. Aunque puede resultar poco convincente, los resultados avalan su uso aunque no haya una teoría clara que los respalde. Cómo trabajar con volúmenes de datos desiguales imbalanced, es un campo actual de investigación.

Hasta ahora hemos defendido que los datos incluidos en el dataset deben reflejar la variación con que aparecen las diferentes clases que el modelo debe aprender.
Sin embargo, pueden darse casos en que directamente no tengamos ejemplos de estas clases para poder introducirlas en el entrenamiento.

Un ejemplo sería intentar detectar una determinada clase (perro) y una clase que no sea igual, es decir, que pueda ser cualquier otra cosa. Si entrenamos con imágenes muy diferentes (por ejemplo, cientos de imágenes de pingüinos o loros), muy probablemente cuando aparezca una clase similar (lobo) la etiquetará erróneamente (como perro).

Para entrenar nuestro modelo adecuadamente hay que introducir suficientes elementos confusers o hard negatives, que son elementos que pueden causar errores de clasificación por similitud entre clases buscadas, con el fin de minimizar estos errores.

“Todos ellos” suele ser la respuesta a la cuestión de la cantidad de datos necesarios. Sin embargo la obtención de estos suele ser compleja, lenta y cara.

El tamaño del dataset de entrenamiento debe ser lo suficientemente grande para conseguir una precisión adecuada, en relación al coste de conseguir los datos.

La cantidad de datos que debemos tener para entrenar adecuadamente nuestro modelo tampoco tiene por qué ser necesariamente enorme. Por norma general, suele haber un incremento exponencial de la precisión del modelo cuando se empieza a entrenar, pero a partir de cierto número de datos de entrada, la precisión aumenta muy poco en comparación con la gran cantidad de datos que se le están introduciendo. El coste de conseguir los datos, puede que no interese asumirlo a partir de ese punto.

También el número de parámetros del modelo cuenta a la hora de definir el tamaño del dataset. Por norma general, será necesario tener un mayor número de muestras que de parámetros, pero existen modelos de aprendizaje profundo que se ajustan muy bien con menos datos de entrenamiento que su número de parámetros. Esto ocurre por ejemplo, cuando hay que diferenciar entre clases muy diferentes.

Antes de comenzar a construir datasets, hay dos situaciones comunes que hay que resolver antes de usar el dataset en un modelo: escalado de atributos features y qué hacer si no se dispone del valor de un atributo.

Cuando los diferentes atributos del vector tiene rangos de valor muy dispares, es necesario normalizarlos para que el modelo funcione correctamente, y no dé más peso a unos atributos que otros sólo por el rango en que se mueven.

Para ellos se siguen los siguientes pasos:

1. Centrado medio: Por cada atributo, se saca su media a partir de todos los datos disponibles, y posteriormente se resta a cada valor de esa característica. Obtenemos valores centrados (alrededor) de 0.
2. Cambiamos la desviación estándar σ a 1: Calculamos la desviación estándar σ de todas las muestras de cada atributo (esto se hace con la media calculada anteriormente). La desviación estándar indica cuánto se desvía cada muestra de su centro. Una vez calculada, se normaliza para cada muestra con la media y desviación típica de ese atributo:

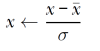
Dado un array x, que representa el dataset (un elemento por cada vector, y cada uno es un array en que cada elemento es un atributo) podemos hacer esto con NumPy de la siguiente forma:

x = (x-x.mean(axis=0))/x.std(axis=0)

Si hiciésemos la media de los valores de cada atributo, obtendríamos valores extremadamente cercanos a cero. Si de igual manera, calculamos la desviación estándar de los valores de cada atributo, obtendríamos valores extremadamente cercanos a 1 . Los valores del dataset ya están normalizados y listos para ser usados en el modelo.

Se puede dar el caso de que en el dataset haya datos que no existan por algún motivo. Sin embargo, el modelo no admite que falten datos, por lo que debemos de asignar un valor, el cual desconocemos.

Una solución es usar valores externos al dataset (fuera de su rango) para que el modelo aprenda a ignorarlos (o de más peso a otras características), o en casos de otros modelos de aprendizaje profundo más avanzados, se pone a cero alguna entrada para “regularizarlo”. Esto es algo que se verá más adelante.

Por ahora, lo que haremos será una solución mucho más obvia: poner como valor la media del resto de valores de esa características, con el fin de que no afecte al esempeño de nuestro modelo. Si el dataset es suficientemente extenso, también podríamos colocar ahí a la moda (valor más común).

El dataset completo no se usa para entrenar un modelo. Hay que dividirlo en al menos 2 partes, idealmente 3:

• Datos de entrenamiento: Serán con los que entrenemos el modelo. Serán la mayor parte del dataset y deberán representar la distribución principal, o “padre” de los datos.
• Datos de test: Se usarán para evaluar lo bien que funciona el modelo. No se usarán para entrenar el modelo, sin no que servirán para evaluarlo después de que éste haya sido entrenado.
• Datos de validación: No todos los modelos lo necesitan, suelen ser útiles con modelos de aprendizaje profundo. La idea es usarlos para evaluar el modelo cuando está siendo entrenado, con el fin de observar el funcionamiento del modelo a lo largo de su entrenamiento, de modo que podamos tomar decisiones acerca del mismo (continuar, darlo por finalizado, cambiar aspectos del entrenamiento o del modelo, etc).

Para modelos de aprendizaje profundo, lo más habitual es dejar el 90% del dataset para datos de entrenamiento, el 5% para datos de validación y otro 5% para datos de test.

Para modelos clásicos, lo más común es usar el 80% de los datos para entrenar el modelo, el 10% como datos de validación y otro 10% como datos de test. Si no se usan datos de validación, los datos de test deben asumir el 20% del total.
Los datos de test grandes, pueden ser apropiados para probar datos que aparecen raramente, pero que “no verlos” (no clasificarlos adecuadamente) puede tener un coste grande.

Podemos generar un dataset “tonto” de prueba con las herramientas de sklearn.

import numpy as np
form sklearn.datasets import make_classification
 
x,y = make_classification(n_samples = 10000, weights=(0.9,0.1))

Obtenemos un array x con 10000 muestras, cada una con 20 atributos (o características).
El array y contiene la etiqueta de clase de cada dato ('0' ó '1'), siendo la primera el 90% del total.

Explicado en El cuaderno de Google Colab

Recordar la importancia de que las diferentes clases aparezcan en la misma proporción que en el mundo real.
Necesitamos crear los diferentes sets de datos para entrenar, validar y testear nuestro modelo, atendiendo a la probabilidad en la que pueden aparecer nuestras clases.
Este particionado se puede hacer de dos maneras: particionando por clase, o por muestreo aleatorio.

Se separan de forma aleatoria los datos en función de las clases y de las proporciones que hemos establecido para los diferentes sets de datos.

En el caso de un dataset de 10000 muestras en el que 9000 están etiquetadas con la clase '0' y 1000 con la clase 1, si deseamos tener unas proporciones: datos de entrenamiento 90%, datos de validación 5%, datos de test 5%, nos quedarán:

• Datos de entrenamiento: 8100 datos aleatorios etiquetados '0' y 900 datos aleatorios etiquetados '1'.
• Datos de validación: 450 datos aleatorios etiquetados '0' y 50 datos aleatorios etiquetados '1'.
• Datos de test: 450 datos aleatorios etiquetados '0' y 50 datos aleatorios etiquetados '1'.

Se puede ver un código de ejemplo en google colab.

Este modo consiste en reordenar el dataset completo de forma aleatoria, y coger las muestras de entrenamiento, validación y test en las proporciones deseadas.
Para usar este método es necesario tener suficientes muestras (podemos considerar 10.000 como suficientes).

El problema que se puede presentar es que no tengamos suficientes muestras en algunos de las subtramas de datos, para localizar las clases que aparecen con menos frecuencia. Esto podría ocurrir si no hubiese un número suficiente de datos. La mejor solución sería conseguir más datos.

Los pasos para extraer las diferentes subtramas de datos serían:

1. Reordenar aleatoriamente el dataset completo.
2. Calcular el número de muestras de entrenamiento y validación, multiplicando el número de muestras totales por la fracción deseada. El resto serán datos de test.
3. Se asignan las primeras muestras del dataset a la subtrama de entrenamiento, según el número calculado en 2.
4. Se asignan las siguientes a la subtrama de validación en el número calculado.
5. El resto se asignan a los datos de set.

Se puede ver el código en el cuaderno de Google Colab

Si los datos son reordenados de forma aleatoria, y los vectores de atributos mantienen el orden, el proceso de particionado de datos en las 3 subtramas debería ser correcto aún con pocos dato o con clases que aparezcan muy pocas veces.

Técnica usada para entrenar y/o seleccionar modelos cuando se tienen pocos datos. Muy útil para los modelos clásicos de aprendizaje automático, ya que los modelos de aprendizaje profundo requieren de muchos datos.

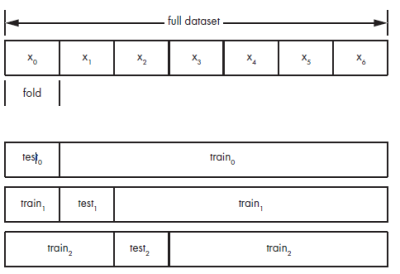
La técnica consiste en dividir el dataset completo, previamente reordenado de forma aleatoria, en diferentes k subtramas no solapadas: x₀, x₁, x₂, …, X_k-1. k es un valor arbitrario, habitualmente entre 5 y 10.

Dejaremos una de las subtramas como datos de test, y el resto como datos de entrenamiento, obviando los datos de validación. El modelo entrenad e este modo será m₀.
Se repite el proceso dejando en cada ocasión una de las subtramas como tatos de test, y obteniendo m₁, m₂, …, m_k-1

Una vez tenemos diferentes instancias de un mismo modelo entrenadas por distintas subtramas de datos, podemos evaluarlas individualmente y realizar la media de sus métricas, para tener una idea de cómo se comportaría con el conjunto de datos completo.

Si tuviésemos diferentes modelos, habría que repetir el proceso con cada uno y ver cuál ofrece mejores resultados. Finalmente el elegido, tendría que ser entrenado con todo el conjunto de datos.

Es sencillo añadir atributos (características) a tus vectores de datos y añadir más y más datos, sin parar a pensar si tiene sentido.
Algunas cosas en las que debemos fijarnos:

• Datos mal etiquetados: El hecho e necesitar miles de datos, hace que la recolección de estos se haga de una forma masiva y sin las suficientes garantías de que el etiquetado sea correcto.
• Datos perdidos: Si en la colección de datos hay algunos atributos desaparecidos de forma puntual, ya vimos que podía hacerse la media con el resto de valores del atributo, con el fin de no perjudicar el entrenamiento. Pero si son muchos los valores faltantes de ese atributo, lo más adecuado es sencillamente eliminarlo. Si existen valores extremos atípicos, también es recomendable borrarlos, ya que afectarán fuertemente al desempeño del modelo.

Si no son demasiados podríamos usar una hoja de cálculo. Si no, podemos hacer un script en python que resuma los datos, o en cualquier programa de cálculo estadístico.

Lo habitual es fijarse en la media aritmética, la desviación estándar, el valor mayor, el valor menor y la mediana (valor intermedio cuando los datos se ordenan de mayor a menor), que tiene por encima y por debajo el mismo número de valores, esto es, el “percentil 50”.
También es interesante fijarse en el “error estándar” (SE en inglés):

El Error Estándar (SE), es la medida de la diferencia entre la media de nuestros valores, y la media de la “distribución padre”. La idea es: “si tenemos más datos, tenemos una mejor idea de la distribución principal que genera nuestros datos, entonces el valor medio de nuestros datos estará más cerca del valor medio de los datos de la distribución padre”.

Si la media y la mediana están “relativamente cerca”, podemos suponer que la distribución de los datos es normal, por lo que sería razonable sustituir los valores inexistentes por la media del resto de valores de ese atributo.

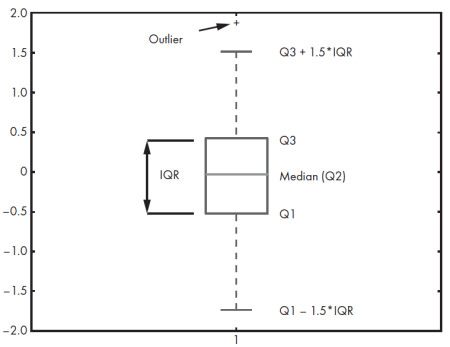
La mejor manera de interpretar los datos, tomando por separado cada atributo, es a través de gráficos de cajas.

• Q1: Final del primer cuartil. El 25% de los valores quedan por debajo.
• Q2: Mediana. Marca del 50% de valores, segundo cuartil.
• Q3: Marca del 75% de los valores, o tercer cuartil.
• IQR: Rango intercuartílico. Se usa para calcular los puntos outlier “lejanos”, o atípicos.
• Outlier: Puntos lejanos del conjunto que no suelen ser tenidos en cuenta.

Las líneas que van de la caja a los puntos extremos que definen el límite de los datos outlier, son convencionalmente llamados “bigotes” (whiskers en inglés, o fliers en la librería Matplotlib de Python).

El análisis que debe hacerse es observar los valores atípicos, por si se corresponden con errores en la entrada de datos y eliminarlos del conjunto (esto debe justificarse de cara a un trabajo serio o publicable). También hay que observar los valores faltantes, por si se correspondiese con algún problema sistemático que lo cause, y si es posible eliminarlos sin introducir un sesgo bias. Al final, lo que impera es el sentido común a la hora de “limpiar” el conjunto de datos.

Se puede ver un ejemplo de programación de este procedimiento en el cuaderno de Google Colab.